1.
For positive integers a and 3, there
exist unique integers q and r such that a = 3q + r, where r must satisfy: 1
(a) 0 ≤ r < 3 (b) 1 < r < 3
(c) 0 < r < 3 (d) 0 < r ≤ 3
Solution: (a)
2.
Find the greatest number of 5 digits,
that will give us the remainder of 5, when divided by 8 and 9 respectively.
(a) 99921 (b) 99931
(c) 99941 (d) 99951
Solution: (c) The greatest number will be
multiple of LCM (8, 9)
LCM of 8 and 9 = 72
On verification, we find that 99941, when divided by 72, leaves remainder 5.
3.
A number 10x + y is multiplied by
another number 10a + b and the result comes as 100p + 10q + r, where r = 2y, q
= 2(x + y) and p = 2x; y < 5, q ≠ 0.
The value of 10a + b may be ________.
2
Solution:
(10x +
y)(10a + b) = 100p + 10q + r
⇒ (10x + y)(10a + b) = 100 × 2x + 10 × 2(x + y) + 2y
⇒ (10x + y)(10a + b) = 200x + 20(x + y) + 2y
⇒ (10x + y)(10a + b) = 220x + 22y
⇒ (10x + y)(10a + b) = 22(10x + y)
⇒ 10a + b = 22
4.
Euclid’s division lemma states for any
two positive integers a and b, there exist integers q and r such that a = bq +
r. If a = 5, b = 8, then write the value of q and r. 1
Solution:
Using Euclid’s division lemma, we get
a = bq + r
5 = 8 × 0 + 5
∴ q = 0 and r = 5
5.
If a and b are two positive integers
such that a = 14b. Find the HCF of a and b.
1
Solution:
We can write
a = 14b + 0
∵ remainder is 0
∴ HCF is b.
6.
For some integers, p and 5, there exist
unique integers q and r such that p = 5q + r. Possible values of r are 1
(a) 0 or 1
(b) 0, 1 or 2
(c) 0, 1, 2 or 3
(d) 0, 1, 2, 3 or 4
Solution:
(d) According to Euclids division lemma,
p = 5q + r, where 0 ≤ r < 5
⇒ r = 0, 1, 2, 3, 4
So, possible values of r are 0, 1, 2, 3 or 4.
7.
If the HCF of 55 and 99 is expressible
in the form 55m – 99, then the value of m is ________. 1
Solution:
55 = 5 × 11, 99 = 9 × 11
∴ HCF(55, 99) = 11
ATQ, 55m – 99 = 11
55 × 2 – 99 = 11
∵ m = 2
8.
If two positive integers a and b are
written as a = x3y2 and b = xy3, where x,
y are prime numbers, then HCF(a, b) is
(a) xy
(b) xy2
(c) x3y3
(d) x2y2
Also, find LCM of (a, b).
Solution:
(b)
Here, a = x3y2 and b = xy3
⇒ a = x × x × x × y × y and b = xy × y × y
∴ HCF(a, b) = x × y × y = x × y2 = xy2
LCM = x3y3
9.
If two positive integers p and q can be
expressed as p = ab2 and q = a3b; where a, b being prime numbers,
then LCM (p, q) is equal to 1
(a) ab (b) a2b2
(c) a3b2 (d) a2b3
Solution:
(c) LCM (p, q) = a3b2
10.
The ratio between the LCM and HCF of 5,
15, 20 is: 1
(a) 9: 1 (b) 4 : 3
(c) 11 : 1 (d) 12 : 1
Solution:
(d) 5, 15 = 5 × 3, 20 = 2 × 2 × 5
LCM(5, 15, 20) = 5 × 3 × 2 × 2 = 60
HCF(5, 15, 20) = 5
11.
Two alarm clocks ring their alarms at
regular intervals of 50 seconds and 48 seconds. If they first beep
together at 12 noon, at what time will they beep again for the first time? 1
(a) 12.20 pm
(b) 12.12 pm
(c) 12.11 pm
(d) none of these
Solution:
(d) LCM of 50 and 48 = 1200
∴ 1200 sec = 20 min
Hence at 12.20 p.m., they will beep again for the first time.
12.
If A = 2n + 13, B = n + 7, where n is a
natural number, then HCF of A and B is: 1
(a) 2 (b) 1
(c) 3 (d) 4
Solution:
(b) Taking different values of n we find that
A and B are coprime.
∴ HCF = 1
13.
There are 576 boys and 448 girls in a school
that are to be divided into equal sections of either boys or girls alone. The
total number of sections thus formed are: 1
(a) 22 (b) 16
(c) 36 (d) 21
Solution:
∴ Number of sections =

14.
The HCF of 2472, 1284 and a third
number N is 12. If their LCM is 23 × 32 × 5 ×
103 × 107, then the number N is: 1
(a) 22 × 32 × 7 (b) 22 × 33 × 103
(c) 22 × 32 × 5 (d) 24 × 32 × 11
Solution:
(c) 2472 = 23 × 3 × 103
1284 = 22 × 3 × 107
∵ LCM = 23 × 32 × 5 × 103 × 107
∴ N = 22 × 32 × 5 = 180
15.
Two natural numbers whose difference is
66 and the least common multiple is 360, are: 1
(a) 120 and 54 (b) 90 and 24
(c) 180 and 114 (d) 130 and 64
Solution:
(b) Difference of 90 and 24 = 66 and LCM of 90
and 24 = 360
∴ Numbers are 90 and 24
16. The HCF and LCM of two numbers are 33 and 264 respectively. When the
first number is completely divided by 2 the quotient is 33. The other number is
________________. 1
Solution:
17.
HCF of 52 × 32 and
35 × 53 is: 1
(a) 53 × 35 (b) 5 × 33
(c) 53 × 32 (d) 52 × 32
Solution:
(d) HCF of 52 × 32 and
35 × 53 = 52 × 32
(c) 5 (d) 6
Solution:
(c) LCM of 7, 8, 11, 12 = 1848
∴ Bells will toll together after every 1848 sec.
∴ In the next 3 hrs, number of times the bells will toll together =
= 5.84
⇒ 5 times.
19. Given that LCM (91, 26) =
182, then HCF (91, 26) is _________. 1
Solution:
LCM (91, 26) × HCF (91, 26) = 91 × 26
182 × HCF (91, 26) = 91 × 26
⇒ HCF (91, 26) =
⇒ HCF (91, 26) = 13
20. The decimal expansion of the rational number 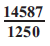
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Solution:
∴ The given rational number will terminate after four decimal places.
21. Which of the following rational numbers have a terminating decimal expansion? 1
Solution:
(c)
The denominator 26 × 52 is of the form 2m × 5n, where m and n are non-negative integers. Hence, it is a terminating decimal expansion.
22.
The decimal expansion of number ![]() has ____________ decimal representation. 1
has ____________ decimal representation. 1
Solution:
The denominator 22 × 53 is
of the form 2m × 5n, where m and n are non-negative
integers. Hence, it has a terminating decimal representation.
23. From the following, the rational number
whose decimal expansion terminating is: 1
Solution:
The denominator 25 × 51 is
of the form 2m × 5n, where m and n are non-negative
integers. Hence, it is a terminating decimal expansion.
24.
For any integer a and
3, there exists unique integers q and r such
that a = 3q + r. Find the possible
values of r. 1
Solution:
According to Euclid's division lemma for two
positive number a and b; there exist integer q and r such
that
a = b × q + r where
0 ≤ r < b
Here b = 3
0 ≤ r < 3
So values of r are 0, 1 or 2.
25. If a and b are two positive integers
such that a = 14b. Find the HCF of a and b. 1
Solution:
We can write
a = 14b + 0
![]() remainder is 0
remainder is 0
![]() HCF
is b.
HCF
is b.
26.
Decompose 32760 into prime factors. 1
Solution:
32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 = 23 ×
32 × 5 × 7 × 13
27. Write the sum of exponents of prime factors
in the prime factorisation of 250. 1
Solution:
250 = 2 × 53
![]() Sum of exponents = 1 + 3 = 4
Sum of exponents = 1 + 3 = 4
28. The HCF of two numbers is 145 and
their LCM is 2175. If one number is 725, then find the other number. 1
Solution:
HCF × LCM = Product of two numbers
![]() 145 × 2175 = 725 ×
other number
145 × 2175 = 725 ×
other number
![]() Other number =
Other number =
= 435

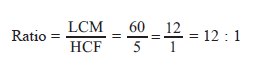




















0 comments:
Post a Comment